Aprende cuántas aristas tiene un prisma triangular y descubre todas sus propiedades fascinantes

Un prisma triangular es un objeto tridimensional que se caracteriza por tener dos bases triangulares y caras laterales formadas por rectángulos. Es un objeto muy utilizado en la geometría y en aplicaciones prácticas como la arquitectura y el diseño de muebles. Conocer la cantidad de aristas que tiene un prisma triangular, así como sus propiedades, es fundamental para comprender su estructura y utilizarlo correctamente en diversas situaciones.

Exploraremos en detalle cuántas aristas tiene un prisma triangular, cómo se calculan y qué papel juegan en la configuración general del prisma. Además, hablaremos sobre las propiedades fascinantes de los prismas triangulares, como su capacidad para apilar y empacar otros sólidos geométricos, su relación con los poliedros regulares y algunas aplicaciones de este tipo de prisma en la vida cotidiana. ¡Prepárate para descubrir el mundo de los prismas triangulares!

Cuántas aristas tiene un prisma triangular y cómo se calculan

Los prismas triangulares son poliedros tridimensionales que se caracterizan por tener una base en forma de triángulo y caras laterales formadas por rectángulos o cuadriláteros. Son especialmente interesantes debido a sus propiedades únicas y su utilidad en diversas áreas, desde matemáticas hasta arquitectura.

Una de las características más importantes de un prisma triangular es el número de aristas que posee. Pero, ¿cómo podemos calcular cuántas aristas tiene un prisma triangular?

Cálculo del número de aristas

Para determinar cuántas aristas tiene un prisma triangular, primero necesitamos entender su estructura básica. Un prisma triangular consta de dos bases triangulares congruentes y tres caras laterales rectangulares.

Cada base triangular tiene tres aristas, lo que da un total de seis aristas para las bases. Estas aristas son compartidas por las caras laterales del prisma. Por lo tanto, cada una de las tres caras laterales comparte dos aristas con las bases, lo que suma un total de seis aristas adicionales.

Sumando las aristas de las bases y las caras laterales, llegamos a la conclusión de que un prisma triangular tiene un total de 12 aristas.

Propiedades fascinantes de los prismas triangulares

Aparte de conocer el número de aristas de un prisma triangular, existen otras propiedades fascinantes relacionadas con su geometría única. Veamos algunas de ellas:

• Volumen: El volumen de un prisma triangular se puede calcular multiplicando el área de la base por la altura del prisma.
• Área de la superficie: La suma del área de las caras laterales y el área de las bases nos da el área total de un prisma triangular.
• Simetría: Un prisma triangular tiene un plano de simetría que divide al prisma en dos mitades congruentes.
• Triángulo equilátero: Si todas las aristas tienen la misma longitud y todos los ángulos son iguales, el prisma triangular se convierte en un prisma regular con una base equilátera.

Estas propiedades hacen que los prismas triangulares sean objetos matemáticos fascinantes y versátiles. Además, su uso en campos como la arquitectura permite crear estructuras estables y estéticamente agradables.

Un prisma triangular tiene un total de 12 aristas y posee una serie de propiedades fascinantes que lo hacen interesante tanto desde el punto de vista matemático como práctico. Conocer estas características nos ayuda a comprender mejor la geometría tridimensional y su utilidad en diferentes disciplinas.

Cuál es la fórmula para calcular el perímetro de un prisma triangular

El perímetro de un prisma triangular se puede calcular sumando la longitud de todos los lados del polígono base y multiplicándolo por la altura del prisma. Un prisma triangular está compuesto por una base triangular y tres caras laterales que se extienden desde cada vértice de la base hasta la parte correspondiente de la base paralela. La fórmula para calcular el perímetro de un prisma triangular es:

Perímetro = (lado1 + lado2 + lado3) * altura

Donde lado1, lado2 y lado3 representan las longitudes de los lados del triángulo base, y altura representa la distancia entre las bases paralelas.

Para ilustrar mejor esto, vamos a ver un ejemplo. Supongamos que tenemos un prisma triangular con un triángulo base equilátero de lado 5 unidades y una altura de 8 unidades. Para calcular el perímetro, simplemente sumamos las longitudes de los lados del triángulo base y luego multiplicamos por la altura:

Perímetro = (5 + 5 + 5) * 8 = 120 unidades

Entonces, el perímetro de este prisma sería de 120 unidades.

Es importante destacar que el perímetro es una medida de longitud y se expresa en la misma unidad que se utiliza para medir los lados del triángulo base y la altura.

Ahora que sabes cómo calcular el perímetro de un prisma triangular, puedes aplicar esta fórmula para resolver problemas geométricos o simplemente para comprender mejor las propiedades y características de estos fascinantes objetos tridimensionales.

Cuáles son las características principales de un prisma triangular

El prisma triangular es un sólido geométrico que se encuentra dentro de la categoría de los poliedros. Se caracteriza por tener dos bases triangulares congruentes y tres caras laterales rectangulares. Una particularidad es que los segmentos de las aristas correspondientes a las bases son perpendiculares a las caras laterales.

Una de las propiedades más fascinantes del prisma triangular es su cantidad de aristas. Para calcular cuántas aristas tiene un prisma triangular, debemos entender su estructura. Cada base está compuesta por tres vértices y tres aristas, mientras que cada cara lateral tiene dos aristas. Por lo tanto, contando todas las aristas de las bases y las caras laterales, podemos determinar cuántas aristas tiene en total un prisma triangular.

Si consideramos cada una de las bases, notamos que tiene tres aristas cada una. Dado que hay dos bases, podemos multiplicar 3 por 2, obteniendo así un total de 6 aristas solo para las bases del prisma triangular.

Luego, concentremos nuestra atención en las caras laterales. Cada una de las tres caras laterales está formada por los segmentos de las aristas correspondientes a las bases y los segmentos perpendiculares a estas aristas. Si observamos con cuidado, podemos notar que hay tres pares de segmentos perpendiculares (uno para cada arista de las bases). Debido a esto, podemos decir que hay seis segmentos perpendiculares en total en todas las caras laterales del prisma triangular.

Ahora, si sumamos los segmentos de las aristas correspondientes a las bases (6) y los segmentos perpendiculares de las caras laterales (6), obtenemos un total de 12 aristas en el prisma triangular.

Por lo tanto, podemos concluir que un prisma triangular tiene exactamente 12 aristas. Esta característica geométrica es fundamental para comprender y visualizar adecuadamente este sólido.

Propiedades adicionales del prisma triangular

Además de la cantidad de aristas, el prisma triangular posee otras propiedades muy interesantes. Al ser un poliedro regular, todas sus caras son congruentes entre sí y todas sus aristas tienen la misma longitud. Esto hace que el prisma triangular sea especialmente simétrico y estéticamente agradable a la vista.

Otra propiedad es que el prisma triangular tiene seis vértices, los cuales están ubicados en las intersecciones de las aristas de las bases con las aristas perpendiculares de las caras laterales. Estos vértices son elementos clave para determinar la forma y estructura del prisma, ya que definen las direcciones de las aristas y caras.

Además, al ser un prisma, también cuenta con una altura. En este caso, la altura se mide desde una base hasta la otra, siguiendo una línea perpendicular a ambas. La altura puede ser utilizada para calcular el volumen del prisma triangular, junto con el área de las bases y el área lateral.

• El volumen del prisma triangular se calcula multiplicando el área de una de las bases por la altura del prisma.
• El área de las bases se obtiene utilizando la fórmula del área de un triángulo: base por altura dividido por 2.
• El área lateral, por otro lado, se determina sumando las áreas de cada una de las caras laterales.

Todas estas características y propiedades hacen que el prisma triangular sea un objeto geométrico sumamente versátil y estudiado. Su estructura y forma única lo convierten en una figura intrigante para los matemáticos, ingenieros y entusiastas de la geometría en general.

Cuáles son las propiedades geométricas de un prisma triangular

Un prisma triangular es un poliedro con una base triangular y caras laterales trapezoidales. Este tipo de prisma tiene características geométricas únicas que lo hacen fascinante y versátil en el campo de la geometría.

Número de aristas

Para comprender completamente las propiedades de un prisma triangular, es fundamental conocer cuántas aristas tiene. Un prisma triangular consta de nueve aristas en total. Esto se debe a que tiene tres aristas en cada uno de sus lados laterales y otras tres aristas que conectan las esquinas de la base triangular con las esquinas opuestas del lado identificado.

Área de la base y área total

Otra propiedad importante de un prisma triangular es su área. Para calcular el área de la base, debemos tomar medidas precisas de los lados del triángulo y aplicar la fórmula adecuada. Una vez calculada el área de la base, podemos determinar el área total del prisma triangular sumando el área de la base y el área de las caras laterales.

La fórmula para calcular el área de la base de un triángulo depende de sus dimensiones: si el triángulo es equilátero, usaremos la fórmula para áreas de triángulos equiláteros; si no es equilátero, utilizaremos la fórmula general para áreas de triángulos.

El área total de un prisma triangular se calcula multiplicando la medida de la base por la altura total del prisma y luego sumando el área de las caras laterales. Esta área total es útil en muchos cálculos que implican volúmenes y superficies.

Longitud de las aristas laterales

Las aristas laterales de un prisma triangular tienen longitudes diferentes a las de la base. Aunque la longitud de cada arista lateral dependerá de las medidas de los lados del triángulo de base, la forma trapezoidal de estas caras laterales garantiza que sean diferentes a los lados del triángulo de base.

Relaciones entre las medidas

Si conocemos algunas de las medidas de un prisma triangular, como la altura, podemos aplicar ciertas fórmulas y relaciones para determinar otras medidas relacionadas, como el área de las caras laterales o el volumen del prisma. Esto hace posible resolver problemas geométricos más complejos e involucra conceptos matemáticos avanzados.

• Por ejemplo, si conocemos el área de la base y la altura de un prisma triangular, podemos calcular su volumen utilizando la fórmula V = Ah, donde A representa el área de la base y h es la altura.
• También podemos utilizar la relación pitagórica para relacionar las dimensiones del triángulo de base con la altura del prisma.
• Además, la medida del perímetro de la base está relacionada con la longitud de las aristas laterales y puede ser utilizada para determinar la longitud de dichas aristas.

Ejemplos de aplicación

La geometría es una ciencia que tiene numerosas aplicaciones en el mundo real. Los prismas triangulares se encuentran en diversos contextos, como la arquitectura, la ingeniería y las artes visuales.

En arquitectura, los prismas triangulares pueden usarse para diseñar techos inclinados o estructuras con formas interesantes. En la ingeniería, estos prismas se emplean para modelar estructuras estables y resistentes a la vez que estéticamente atractivas.

Asimismo, en el arte, los prismas triangulares son una forma de representación visual tridimensional que permite crear ilusiones ópticas y juegos de luces y sombras. Además, su geometría única puede ser utilizada para crear efectos asombrosos en obras de arte escultórico y arquitectónico.


// Ejemplo de cálculo del área de la base de un prisma triangular
baseTriangulo = 8 cm;
alturaTriangulo = 6 cm;

areaBase = (baseTriangulo * alturaTriangulo) / 2;


Las propiedades geométricas de un prisma triangular son fundamentales para comprender este objeto tridimensional. Desde el número de aristas hasta las relaciones entre las medidas, cada aspecto juega un papel importante en el estudio y aplicación de este poliedro en diversas disciplinas.

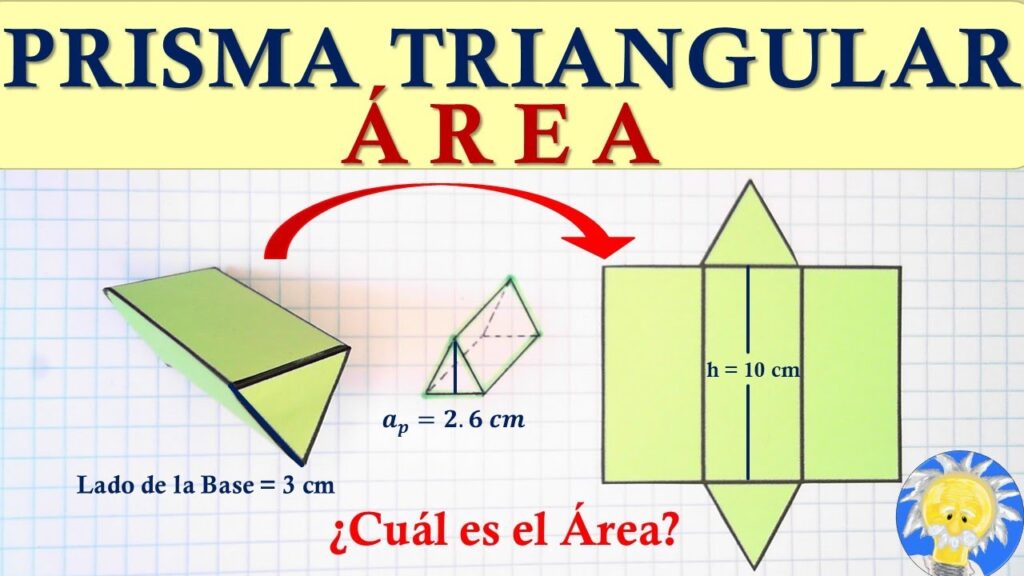
Cómo se determina el área de la base de un prisma triangular

El área de la base de un prisma triangular se puede determinar utilizando la fórmula adecuada. En el caso de un prisma triangular, la base es un triángulo y el área se calcula multiplicando la longitud de la base por la altura del triángulo y dividiendo el resultado por 2. La fórmula sería la siguiente:

Área base = (base * altura) / 2

Para obtener el valor de la base, debemos conocer la longitud de uno de los lados del triángulo base del prisma triangular. Si todos los lados del triángulo son iguales, podemos llamar a este lado "a". Entonces, el valor de la base será igual a "a".

Por otro lado, para determinar la altura del triángulo base, necesitamos conocer la longitud de una de las alturas del triángulo. Si el prisma es equilátero, todas las alturas serán iguales, y llamaremos a esta altura "h". Entonces, el valor de la altura será igual a "h".

Para calcular el área de la base de un prisma triangular, debemos multiplicar la longitud de uno de los lados del triángulo base por la longitud de una de las alturas del triángulo y dividir el resultado por 2.

Una vez que hayamos determinado el área de la base, podemos utilizarla junto con la altura total del prisma para calcular su área superficial y su volumen. Estas propiedades fascinantes nos permiten comprender mejor la geometría del prisma y sus aplicaciones en varios campos, como la arquitectura, la ingeniería y las ciencias naturales.

De qué manera se calcula el volumen de un prisma triangular

Calcular el volumen de un prisma triangular puede resultar algo confuso si no se conocen las fórmulas adecuadas. Sin embargo, con un poco de paciencia y comprensión, es posible determinar el volumen de este sólido geométrico de forma sencilla.

Para calcular el volumen de un prisma triangular, se debe multiplicar el área de la base por la altura. Pero, ¿cómo se obtiene el área de la base en un prisma triangular? La respuesta es aplicando la fórmula del área de un triángulo.

Cálculo del área de un triángulo

La fórmula general para calcular el área de cualquier triángulo es:

Área = (base * altura) / 2

En el caso de un prisma triangular, la base es un triángulo equilátero, lo que significa que todos sus lados tienen la misma medida. Supongamos que esa medida es "a".

La altura del triángulo equilátero se puede obtener aplicando el teorema de Pitágoras, considerando a uno de los lados como la hipotenusa y dividiendo ese lado por 2 como el cateto opuesto. Por lo tanto:

Altura = (√3/2) * a

Sustituyendo el valor de la altura en la fórmula del área del triángulo, obtenemos:

Área = (a * (√3/2) * a) / 2
Área = (a^2 * √3) / 4

Una vez calculado el área de la base, se debe multiplicar por la altura del prisma para obtener su volumen. Supongamos que la altura del prisma es "h". Entonces:

Volumen = Área * h
Volumen = ((a^2 * √3) / 4) * h

Como resultado final, el volumen de un prisma triangular se calcula multiplicando el área de la base por la altura del prisma:

Volumen = (a^2 * √3 * h) / 4

Ahora que conoces la fórmula para calcular el volumen de un prisma triangular, puedes aplicarla en cualquier problema que involucre este sólido geométrico. Recuerda siempre sustituir los valores correspondientes a cada medida para obtener el resultado correcto.

Cuál es la relación entre las aristas, vértices y caras de un prisma triangular

Para comprender cuántas aristas tiene un prisma triangular y su relación con los vértices y caras, es importante tener claro qué es un prisma triangular en primer lugar.

Un prisma triangular es un poliedro que consta de dos bases triangulares paralelas, conectadas por caras laterales rectangulares. Estas caras laterales son rectángulos ya que sus lados opuestos son paralelos y de igual longitud.

Cantidad de aristas

La cantidad de aristas de un prisma triangular depende de su tamaño y forma específica. Para determinar este número, debemos analizar las características del prisma.

Un prisma triangular tiene tres aristas en cada una de sus bases triangulares. Además, cada una de estas aristas se conecta con otra mediante una arista lateral. Por lo tanto, si consideramos las dos bases y las caras laterales, podemos decir que un prisma triangular tiene un total de 9 aristas.

Cantidad de vértices

Los vértices son los puntos donde las aristas de un prisma triangular se intersectan. Para contar la cantidad de vértices de un prisma triangular, debemos analizar cómo se encuentran las aristas y las bases.

En cada base triangular, hay tres vértices donde se encuentran las aristas. Además, en un prisma triangular, cada una de las aristas laterales se conecta con una arista de cada base. Esto significa que hay otros tres vértices adicionales en las aristas laterales.

Por lo tanto, sumando los vértices de las bases y los de las aristas laterales, encontramos que un prisma triangular tiene un total de 6 vértices.

Cantidad de caras

Las caras de un prisma triangular son las superficies planas que lo delimitan. Para determinar la cantidad de caras de un prisma triangular, debemos analizar sus bases y las caras laterales.

Un prisma triangular tiene dos bases triangulares, por lo que cuenta con dos caras de este tipo. Además, hay tres caras laterales rectangulares que conectan las bases entre sí. Por lo tanto, podemos decir que un prisma triangular tiene un total de 5 caras.

• Un prisma triangular tiene un total de 9 aristas.
• Un prisma triangular cuenta con 6 vértices.
• Un prisma triangular tiene 5 caras en total.

El número de aristas, vértices y caras de un prisma triangular depende de su estructura geométrica específica, pero en general, podemos determinar que tiene 9 aristas, 6 vértices y 5 caras. Estas propiedades fascinantes hacen del prisma triangular un objeto de estudio interesante en matemáticas y geometría.

Existen diferentes tipos de prismas triangulares

Los prismas triangulares son figuras tridimensionales fascinantes que se caracterizan por tener una base triangular y caras laterales también triangulares. Son ampliamente estudiados en la geometría, ya que presentan propiedades únicas y pueden ser encontrados en diversas formas y tamaños.

Dentro de los diferentes tipos de prismas triangulares se encuentran:

Prisma recto

Un prisma triangular recto es aquel cuyas caras laterales son rectángulos y las bases son triángulos rectángulos. Todas las aristas son perpendiculares a las bases y las caras laterales tienen la misma altura que las bases.

Prisma oblicuo

El prisma triangular oblicuo presenta caras laterales que no son perpendiculares a las bases. Esto significa que las aristas no son ortogonales y se intersectan en ángulos distintos a 90 grados.

Prisma regular

Un prisma triangular regular se caracteriza por tener todas sus caras laterales congruentes entre sí y del mismo tamaño. Además, todas las aristas tienen la misma longitud y las bases son triángulos equiláteros.

Además de estos tipos, existen muchas otras variantes de prismas triangulares, cada uno con características y propiedades específicas. Estos prismas pueden tener diferentes números de aristas, lo cual determina su forma y estructura. A continuación, exploraremos más a fondo las aristas de un prisma triangular y descubriremos cuántas pueden tener dependiendo de sus características geométricas.

Cuáles son las aplicaciones prácticas de los prismas triangulares en la vida cotidiana

Los prismas triangulares son sólidos geométricos fascinantes con múltiples aplicaciones prácticas en nuestra vida cotidiana. Su forma triangular única y sus propiedades los hacen ideales para una variedad de usos en diferentes campos y situaciones.

Arquitectura

En el campo de la arquitectura, los prismas triangulares son ampliamente utilizados para crear estructuras estables y estéticamente agradables. Debido a su forma, pueden soportar cargas y distribuir el peso de manera uniforme, lo que los convierte en elementos fundamentales en la construcción de puentes, edificios y otras obras civiles. Además, su diseño triangular puede proporcionar un aspecto moderno y llamativo a las fachadas de los edificios.

Óptica

En el ámbito de la óptica, los prismas triangulares desempeñan un papel crucial en la descomposición de la luz y la formación de espectros. Al pasar por un prisma triangular, la luz se refracta y se divide en los colores del arcoíris debido al fenómeno de dispersión. Esta propiedad es aprovechada en dispositivos como prismáticos, telescopios y cámaras fotográficas para obtener imágenes nítidas y claras.

Mecánica

En la industria mecánica, los prismas triangulares también encuentran aplicaciones importantes. Por ejemplo, en maquinarias CNC (control numérico computarizado), los prismas triangulares se utilizan para medir y controlar la posición y movimiento de los diferentes ejes de la máquina. Además, en mecanismos de transmisión de potencia, los prismas triangulares con superficies reflectantes pueden cambiar la dirección de la fuerza transmitida sin alterar el sentido del movimiento.

Matemáticas y geometría

Por supuesto, no podemos olvidar mencionar las aplicaciones de los prismas triangulares en el campo de las matemáticas y la geometría. Su forma única y sus propiedades geométricas son fundamentales para el estudio y comprensión de figuras espaciales más complejas. Los prismas triangulares son utilizados en actividades educativas para enseñar conceptos como áreas laterales, volúmenes y relaciones de congruencia entre distintas caras.

Diseño de joyas

Por último, pero no menos importante, los prismas triangulares son muy utilizados en el diseño de joyas. Su forma elegante y moderna los convierte en una opción popular para la creación de colgantes, pendientes y pulseras. Además, debido a su capacidad de refracción de la luz, los prismas triangulares en forma de gemas o piedras preciosas pueden crear hermosos efectos de brillo y luminosidad.

Los prismas triangulares tienen numerosas aplicaciones prácticas en nuestra vida cotidiana. Ya sea en arquitectura, óptica, mecánica, matemáticas o incluso en el diseño de joyas, estos sólidos geométricos demuestran su versatilidad y utilidad en diferentes campos. Explorar todas las propiedades de los prismas triangulares puede abrirnos a un mundo de posibilidades creativas y funcionales.

Cuál es la diferencia entre un prisma triangular y otros poliedros

Los prismas triangulares son una forma particular de poliedros que se caracterizan por tener dos bases triangulares congruentes y tres caras laterales rectangulares. A diferencia de otros poliedros, como los cubos o las pirámides, los prismas triangulares no tienen caras con forma de pentágonos, hexágonos u otras figuras poligonales.

Esta diferencia en la geometría de los prismas triangulares tiene un impacto significativo en sus propiedades y características. Por ejemplo, la cantidad de aristas de un prisma triangular está directamente relacionada con su forma única. Pero, ¿cuántas aristas tiene exactamente un prisma triangular?

Cuántas aristas tiene un prisma triangular

Para determinar la cantidad de aristas de un prisma triangular, necesitamos analizar su estructura. Como mencionamos anteriormente, los prismas triangulares tienen dos bases triangulares congruentes y tres caras laterales rectangulares.

Cada una de las bases triangulares está formada por tres segmentos rectos (los lados del triángulo), lo que nos da un total de seis aristas. Por otro lado, cada cara lateral rectangular está formada por dos segmentos rectos horizontales y dos verticales, sumando un total de cuatro aristas por cada cara lateral.

Entonces, si tenemos tres caras laterales rectangulares, multiplicamos el número de aristas por cara lateral (4) por el número de caras laterales (3), lo que nos da un total de 12 aristas para las caras laterales.

Finalmente, sumamos las aristas de las bases (6) con las de las caras laterales (12), obteniendo así un total de 18 aristas para un prisma triangular.

Propiedades fascinantes de los prismas triangulares

Además de su cantidad de aristas, los prismas triangulares tienen otras propiedades fascinantes que vale la pena mencionar. Algunas de estas propiedades incluyen:

1. Simetría axial: Los prismas triangulares tienen líneas de simetría que dividen al prisma en dos partes congruentes. Estas líneas pasan por el centro del prisma y por puntos medios de las aristas de las bases.
2. Área de superficie: La fórmula para calcular el área de la superficie de un prisma triangular es 2(área de la base) + perímetro de la base x altura del prisma.
3. Volumen: El volumen de un prisma triangular se calcula multiplicando el área de la base por la altura del prisma.
4. Relación con otros poliedros: Los prismas triangulares son poliedros regulares, es decir, sus caras son polígonos regulares y sus ángulos son todos iguales.

Los prismas triangulares son poliedros fascinantes con una estructura particularmente única y propiedades interesantes. Su cantidad de aristas, siendo 18, los distingue de otros poliedros y su simetría axial, área de superficie, volumen y relación con otros poliedros los convierten en un tópico apasionante para el estudio de la geometría.

Preguntas frecuentes (FAQ)

1. ¿Cuántas aristas tiene un prisma triangular?

Un prisma triangular tiene 9 aristas en total.

2. ¿Cuántas caras tiene un prisma triangular?

Un prisma triangular tiene 5 caras en total: 2 bases triangulares y 3 caras laterales rectangulares.

3. ¿Cuáles son las propiedades de un prisma triangular?

Las propiedades de un prisma triangular incluyen tener 3 vértices, 6 aristas y 5 caras.

4. ¿Cómo se calcula el volumen de un prisma triangular?

Para calcular el volumen de un prisma triangular, se multiplica el área de la base por la altura del prisma.

5. ¿Cuál es la fórmula del área lateral de un prisma triangular?

La fórmula del área lateral de un prisma triangular es: Ap = p × a, donde Ap es el área lateral, p es el perímetro de la base triangular y a es la apotema del prisma.