Descubre las 5 poderosas razones trigonométricas recíprocas para resolver cualquier problema

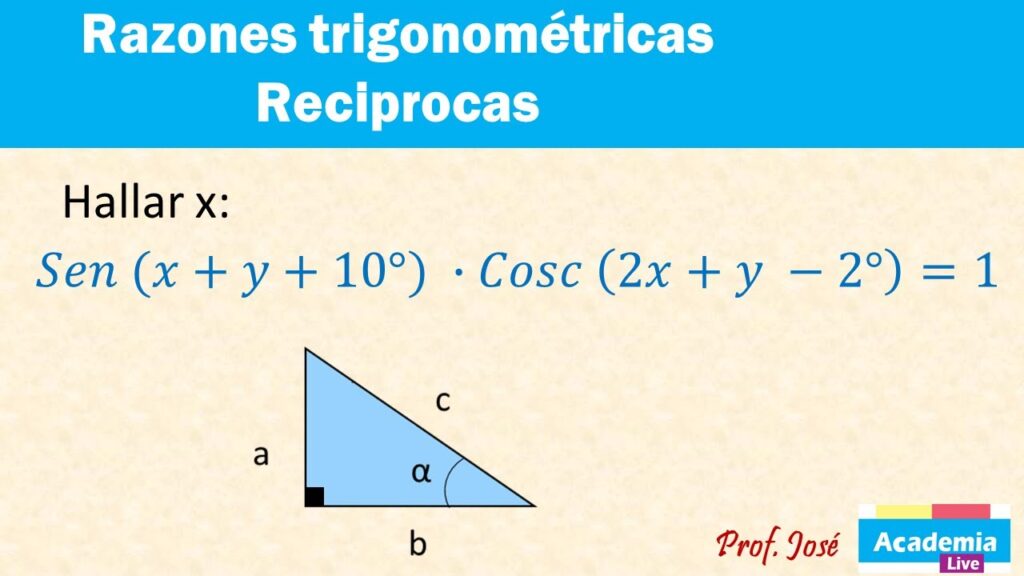
La trigonometría es una de las ramas fundamentales de las matemáticas que se encarga de estudiar las relaciones y propiedades de los triángulos. Las razones trigonométricas son herramientas importantes en esta disciplina y nos permiten resolver problemas relacionados con las medidas de los ángulos y los lados de un triángulo.

Exploraremos las 5 poderosas razones trigonométricas recíprocas. Estas razones son el seno recíproco, el coseno recíproco, la tangente recíproca, la cosecante recíproca y la cotangente recíproca. Veremos cómo estas razones se relacionan entre sí y cómo pueden ser utilizadas para resolver diferentes tipos de problemas trigonométricos.

¿Qué es una razón trigonométrica recíproca y por qué es importante conocerla?

Las razones trigonométricas recíprocas son una herramienta fundamental en la resolución de problemas relacionados con ángulos y triángulos. Estas razones son el complemento de las razones trigonométricas tradicionales, y nos permiten obtener información adicional que puede facilitar la resolución de los mismos.

En matemáticas, las razones trigonométricas se definen como el cociente entre dos lados de un triángulo rectángulo y se utilizan para describir las relaciones entre los ángulos y los lados del triángulo.

Las 5 poderosas razones trigonométricas recíprocas

• cosecante (csc): Esta razón recíproca es el cociente entre la hipotenusa y el cateto opuesto del triángulo rectángulo. La csc nos indica cuántas veces una línea perpendicular a un lado del triángulo puede caber en la hipotenusa. Es útil en el cálculo de la longitud de un lado desconocido cuando conocemos un ángulo y su cateto opuesto.
• secante (sec): Se define como el cociente entre la hipotenusa y el cateto adyacente del triángulo rectángulo. La sec nos permite determinar cuántas veces una línea perpendicular puede ajustarse en el cateto adyacente. Es especialmente útil cuando necesitamos encontrar la longitud de un lado desconocido cuando conocemos un ángulo y su cateto adyacente.
• cotangente (cot): La cotangente es el cociente entre el cateto adyacente y la longitud del cateto opuesto del triángulo rectángulo. Esta razón trigonométrica recíproca nos indica cuántas veces una línea perpendicular puede ajustarse en el cateto adyacente. La cotangente se utiliza principalmente para calcular ángulos o encontrar la longitud de un lado desconocido cuando conocemos el cateto adyacente.
• verseno (vers): Es el complemento del seno. El verseno se obtiene restando el valor del seno de 1. Nos proporciona información complementaria sobre la relación entre los ángulos y los lados del triángulo rectángulo.
• vercoseno (verc): La vercoseno es similar al coseno, pero su valor se obtiene al restar el coseno de 1. Al igual que el verseno, proporciona información adicional sobre la relación entre los ángulos y los lados del triángulo rectángulo.

Conocer las razones trigonométricas recíprocas nos permite tener una visión más completa y detallada de los triángulos y los ángulos. Estas poderosas herramientas nos ayudan a resolver problemas de manera eficiente y precisa, ampliando nuestro conocimiento y capacidad para trabajar con figuras geométricas en diversas situaciones.

¿Cuáles son las 5 poderosas razones trigonométricas recíprocas que debes saber?

Las razones trigonométricas recíprocas son un conjunto de funciones matemáticas que están relacionadas entre sí y son muy útiles para resolver problemas que involucran triángulos. Estas razones se definen en términos de las funciones trigonométricas básicas, como el seno, el coseno y la tangente.

A continuación, descubrirás las 5 poderosas razones trigonométricas recíprocas que debes conocer:

Razón trigonométrica recíproca del seno (cosecante)

La cosecante es la razón trigonométrica recíproca del seno. Su valor se calcula como el inverso del seno de un ángulo dado. Es decir, si el seno de un ángulo es A, la cosecante de ese ángulo será 1/A. La cosecante está relacionada con los catetos de un triángulo rectángulo y su hipotenusa.

Razón trigonométrica recíproca del coseno (secante)

La secante es la razón trigonométrica recíproca del coseno. Se obtiene calculando el inverso del coseno de un ángulo específico. Si el coseno de un ángulo es B, entonces la secante de ese ángulo será 1/B. La secante también está relacionada con los lados de un triángulo rectángulo.

Razón trigonométrica recíproca de la tangente (cotangente)

La cotangente es la razón trigonométrica recíproca de la tangente. Se calcula tomando el inverso de la tangente de un ángulo en particular. Si la tangente de un ángulo es C, entonces la cotangente de ese ángulo será 1/C. La cotangente está relacionada con los catetos del triángulo rectángulo.

Razón trigonométrica recíproca del ángulo explementario

El ángulo explementario es aquel que, sumado a otro ángulo A, forma un ángulo de 90 grados (o pi/2 radianes). La razón trigonométrica recíproca del ángulo explementario es igual a la razón trigonométrica del ángulo original. Por ejemplo, si la sine de un ángulo A es D, entonces la cosine del ángulo explementario de A también será D.

Razón trigonométrica recíproca del ángulo complementario

El ángulo complementario es aquel que, sumado a otro ángulo E, forma un ángulo de 180 grados (o pi radianes). Al igual que el explementario, la razón trigonométrica recíproca del ángulo complementario es igual a la razón trigonométrica del ángulo original. Por ejemplo, si la tangent de un ángulo E es F, entonces la cotangent del ángulo complementario de E también será F.

Estas 5 poderosas razones trigonométricas recíprocas son fundamentales para resolver cualquier problema relacionado con triángulos y ángulos. Su comprensión adecuada te permitirá abordar desafíos matemáticos más complejos y brindarte una comprensión más profunda de la trigonometría.

¿Cómo se utiliza la razón trigonométrica recíproca para resolver problemas trigonométricos?

Para resolver problemas trigonométricos, es fundamental tener un buen dominio de las razones trigonométricas recíprocas. Estas razones son el complemento y el suplemento de las razones trigonométricas básicas, y se utilizan ampliamente en la resolución de diferentes tipos de problemas.

La razón trigonométrica recíproca de un ángulo está definida como el cociente entre el cateto opuesto y la hipotenusa (en el caso de las funciones seno y cosecante) o entre el cateto adyacente y la hipotenusa (en el caso de las funciones coseno y secante).

Razón trigonométrica recíproca del seno: cosecante

La función cosecante, abreviada como csc, es la razón trigonométrica recíproca del seno. Se define como el cociente entre la hipotenusa y el cateto opuesto a un ángulo en un triángulo rectángulo.

La función csc(x) = 1/sen(x), lo que significa que si conocemos el valor de la función seno de un ángulo, podemos calcular su función cosecante utilizando la fórmula mencionada anteriormente.

La función cosecante tiene algunas propiedades importantes que nos permiten resolver problemas trigonométricos más complejos. Por ejemplo, la función csc tiene una periodicidad de π, por lo que csc(x) = csc(x + nπ), donde n es cualquier número entero.

Razón trigonométrica recíproca del coseno: secante

La función secante, abreviada como sec, es la razón trigonométrica recíproca del coseno. Se define como el cociente entre la hipotenusa y el cateto adyacente a un ángulo en un triángulo rectángulo.

La función sec(x) = 1/cos(x), lo que significa que si conocemos el valor de la función coseno de un ángulo, podemos calcular su función secante utilizando la fórmula mencionada anteriormente.

Al igual que la función cosecante, la función secante también tiene propiedades útiles para resolver problemas trigonométricos. La función sec tiene una periodicidad de 2π, por lo que sec(x) = sec(x + 2nπ), donde n es cualquier número entero.

Aplicaciones de las razones trigonométricas recíprocas

Las razones trigonométricas recíprocas juegan un papel fundamental en la resolución de problemas trigonométricos más complejos. Estas funciones nos permiten obtener información adicional sobre los ángulos y lados de un triángulo rectángulo, lo cual es especialmente útil en problemas de navegación, astronomía, arquitectura y otras disciplinas.

Además, las razones trigonométricas recíprocas también se utilizan en el cálculo de límites y derivadas de funciones trigonométricas inversas, así como en diversas aplicaciones de la física y la ingeniería.

Cuidado con las restricciones

Es importante tener en cuenta que las funciones cosecante y secante están definidas únicamente para ángulos diferentes de 0 y π, ya que en estos valores las razones trigonométricas se vuelven indefinidas.

Por lo tanto, al utilizar las razones trigonométricas recíprocas, es necesario asegurarse de que los ángulos involucrados no sean múltiplos de π o cero, de lo contrario las funciones perderán su significado.

Las razones trigonométricas recíprocas son herramientas poderosas para resolver problemas trigonométricos. Nos permiten obtener información adicional sobre los triángulos rectángulos y aplicarla en diversas situaciones prácticas. Sin embargo, es importante recordar las restricciones asociadas a estas funciones y estar atentos a su dominio para evitar errores en nuestros cálculos.

¿Cuáles son los beneficios de utilizar las razones trigonométricas recíprocas en lugar de las regulares?

Las razones trigonométricas recíprocas son poderosas herramientas que nos permiten resolver problemas de trigonometría de manera más eficiente y precisa. Estas razones, también conocidas como funciones trigonométricas inversas, se definen a partir de las razones trigonométricas básicas: seno, coseno y tangente.

Razón trigonométrica recíproca del seno (cosecante)

La razón trigonométrica recíproca del seno, también llamada cosecante, se define como el inverso del seno de un ángulo. Se representa como csc(x) y se calcula mediante la fórmula csc(x) = 1 / sin(x). Esta función es especialmente útil cuando necesitamos encontrar el valor del ángulo dado su seno.

Razón trigonométrica recíproca del coseno (secante)

La razón trigonométrica recíproca del coseno, conocida como secante, es el inverso del coseno de un ángulo. Se denota como sec(x) y se obtiene aplicando la fórmula sec(x) = 1 / cos(x). La función secante es muy útil para determinar el valor del ángulo cuando se conoce el valor de su coseno.

Razón trigonométrica recíproca de la tangente (cotangente)

La razón trigonométrica recíproca de la tangente, llamada cotangente, se define como el inverso de la tangente de un ángulo. Se representa como cot(x) y se calcula usando la fórmula cot(x) = 1 / tan(x). Esta función nos ayuda a encontrar el valor del ángulo cuando se conoce su tangente.

Beneficios de utilizar las razones trigonométricas recíprocas

Ahora que conocemos las definiciones de las razones trigonométricas recíprocas, veamos cuáles son los beneficios de utilizarlas en lugar de las razones trigonométricas regulares:

• Mayor precisión: Las razones trigonométricas recíprocas proporcionan resultados más precisos debido a que utilizan los valores inversos de las funciones trigonométricas básicas. Esto es especialmente importante cuando trabajamos con ángulos pequeños o muy cercanos a los límites de las funciones trigonométricas.
• Simplificación de cálculos: Al utilizar las razones trigonométricas recíprocas, podemos simplificar cálculos complejos, ya que en muchas ocasiones necesitaremos calcular el valor inverso de alguna función trigonométrica. En lugar de calcular la función trigonométrica regular y luego su inverso, directamente podemos utilizar la función trigonométrica recíproca correspondiente.
• Mejor comprensión: El uso de las razones trigonométricas recíprocas nos permite tener una visión más completa y profunda de los conceptos trigonométricos. Al entender cómo se relacionan entre sí las diferentes razones trigonométricas, podemos expandir nuestro conocimiento y desarrollar una comprensión más sólida de la materia.
• Mayor flexibilidad: Al dominar las razones trigonométricas recíprocas, tenemos un conjunto más amplio de herramientas para resolver problemas de trigonometría. Esto nos da una mayor flexibilidad a la hora de abordar diferentes situaciones y nos permite encontrar soluciones alternativas a los problemas que se nos presenten.
• Aplicación en campos avanzados: Las razones trigonométricas recíprocas son fundamentales en campos como la física, la ingeniería y la geometría. Estas funciones nos permiten analizar fenómenos naturales, diseñar estructuras eficientes y modelar formas y figuras complejas. Con un buen dominio de las razones trigonométricas recíprocas, podemos expandir nuestras habilidades y abrirnos a nuevas oportunidades profesionales.

Utilizar las razones trigonométricas recíprocas nos brinda ventajas significativas a la hora de resolver problemas matemáticos. Ya sea buscando mayor precisión, simplificación de cálculos, mejor comprensión, mayor flexibilidad o aplicaciones en campos avanzados, estas poderosas herramientas nos ayudan a resolver cualquier problema trigonométrico con eficiencia y precisión.

Cómo puedes aplicar las razones trigonométricas recíprocas en situaciones de la vida cotidiana

Las razones trigonométricas recíprocas son conceptos matemáticos que resultan de gran utilidad en diversas situaciones de la vida cotidiana. Estas razones se definen como el cociente entre las longitudes de los diferentes lados de un triángulo rectángulo, y nos permiten resolver una amplia variedad de problemas relacionados con ángulos y distancias.

1. La razón cosecante (csc)

La razón cosecante se define como el cociente entre la hipotenusa y el cateto adyacente a un ángulo en un triángulo rectángulo. Esta razón nos permite determinar la longitud de un lado desconocido sabiendo la medida de un ángulo y la longitud de otro lado del triángulo. Por ejemplo, si conocemos la medida de un ángulo y la hipotenusa, podemos usar la razón cosecante para calcular la longitud del cateto adyacente.

2. La razón secante (sec)

La razón secante se define como el cociente entre la hipotenusa y el cateto opuesto a un ángulo en un triángulo rectángulo. Esta razón nos permite determinar la longitud de un lado desconocido sabiendo la medida de un ángulo y la longitud de otro lado del triángulo. Por ejemplo, si conocemos la medida de un ángulo y la hipotenusa, podemos usar la razón secante para calcular la longitud del cateto opuesto.

3. La razón cotangente (cot)

La razón cotangente se define como el cociente entre el cateto adyacente y el cateto opuesto a un ángulo en un triángulo rectángulo. Esta razón nos permite determinar la medida de un ángulo desconocido sabiendo la longitud de los dos catetos del triángulo. Por ejemplo, si conocemos la longitud de los catetos, podemos usar la razón cotangente para calcular la medida del ángulo.

4. La razón tangente (tan)

La razón tangente se define como el cociente entre el cateto opuesto y el cateto adyacente a un ángulo en un triángulo rectángulo. Esta razón nos permite determinar la medida de un ángulo desconocido sabiendo la longitud de los dos catetos del triángulo. Por ejemplo, si conocemos la longitud de los catetos, podemos usar la razón tangente para calcular la medida del ángulo.

5. La razón seno (sen)

La razón seno se define como el cociente entre el cateto opuesto y la hipotenusa de un triángulo rectángulo. Esta razón nos permite determinar la medida de un ángulo desconocido sabiendo la longitud de un cateto y la hipotenusa del triángulo. Por ejemplo, si conocemos la longitud de un cateto y la hipotenusa, podemos usar la razón seno para calcular la medida del ángulo.

Las razones trigonométricas recíprocas son herramientas poderosas que nos permiten resolver una amplia variedad de problemas relacionados con ángulos y distancias. Su aplicación se extiende desde la navegación marítima hasta el diseño arquitectónico. Estas razones nos brindan una comprensión más profunda de las propiedades matemáticas de los triángulos rectángulos, lo que nos permite resolver problemas de manera eficiente y precisa.

Las razones trigonométricas recíprocas son el inverso de las razones trigonométricas originales. Por ejemplo, el seno recíproco de un ángulo es igual a 1 dividido entre el valor del seno original.

Las cinco razones trigonométricas recíprocas son: cosecante, secante, cotangente, coseno recíproco y seno recíproco.

Las razones trigonométricas recíprocas se utilizan para resolver problemas trigonométricos más complejos y encontrar relaciones entre diferentes ángulos.

Para calcular las razones trigonométricas recíprocas, simplemente se toma el inverso de la razón trigonométrica original. Por ejemplo, si el seno de un ángulo es igual a 0.5, entonces su seno recíproco será 1/0.5 = 2.

Las razones trigonométricas recíprocas están estrechamente relacionadas con las identidades trigonométricas, ya que se pueden derivar a partir de ellas. Las razones recíprocas son útiles para simplificar expresiones y resolver ecuaciones en trigonometría.